Resistors in Series
When
resistors are connected one after each other this is called connecting in series. This is shown below.

To calculate the total overall resistance of a number of resistors connected in this way you add up the individual resistances. This is done using the following formula:
Rtotal = R1 + R2 +R3 and so on. Example: To calculate the total resistance for these three resistors in series.
 |
Rtotal = R1 + R2 + R3 = 100 + 82 + 1 Ohms = 183 Ohms
|
Task 1:
Calculate the total resistance of the following resistor in series.
 |
Rtotal |
= _______________ |
| = _______________ |
 |
Rtotal |
= _______________ |
| = _______________ |
 |
Rtotal |
= _______________ |
| = _______________ |
Resistors in Parallel
When resistors are connected across each other (side by side) this is called connecting in parallel. This is shown below.

Two Resistors in Parallel
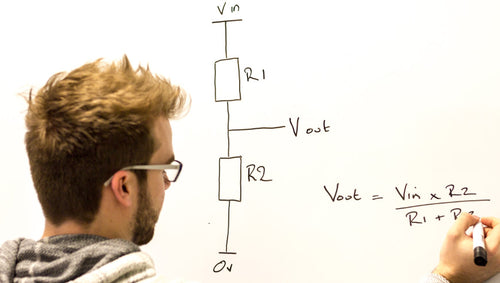
| To calculate the total overall resistance of a of two resistors connected in this way you can use the following formula: |
 |
Example: To calculate the total resistance for these two resistors in parallel.

Task 2:
Calculate the total resistance of the following resistor in parallel.

Three or more resistors in parallel

To calculate the total overall resistance of a number of three or more resistors connected in this way you can use the following formula:

Example: To calculate the total resistance for these three resistors in parallel

Task 3:
Calculate the total resistance of the following resistor in parallel.

Answers
Task 1
1 = 1492 Ohms 2 = 2242 Ohms 3 = 4847 Ohms
Task 2
1 = 5 Ohms 2 = 9.57 Ohms 3 = 248.12 Ohms
Task 3
1 = 5.95 Ohms 2 = 23.76 Ohms Download a pdf version of this page
here 
Learn more about the author
read more »
©Kitronik Ltd – You may print this page & link to it, but must not copy the page or part thereof without Kitronik's prior written consent.
 To calculate the total overall resistance of a number of resistors connected in this way you add up the individual resistances. This is done using the following formula: Rtotal = R1 + R2 +R3 and so on. Example: To calculate the total resistance for these three resistors in series.
To calculate the total overall resistance of a number of resistors connected in this way you add up the individual resistances. This is done using the following formula: Rtotal = R1 + R2 +R3 and so on. Example: To calculate the total resistance for these three resistors in series.







 To calculate the total overall resistance of a number of three or more resistors connected in this way you can use the following formula:
To calculate the total overall resistance of a number of three or more resistors connected in this way you can use the following formula:  Example: To calculate the total resistance for these three resistors in parallel
Example: To calculate the total resistance for these three resistors in parallel 








29 comments
Jhayvir
What is the equivalent resistance of the three resistors in series with the following values: R1 = 10 Ω, R2 = 20 Ω, and R3 = 5 Ω (Give only the numeric part of your answer.)
Can u guys hep me? Please thanks for the response :>
Mark Donnison
Hi, without seeing how your classmate is arriving at an answer it is impossible to say. However, this is the correct way and if you do it this way you know that you will arrive at the correct answer. I hope this helped.
Thea
Hi! I'm confused because the method my classmate use in solving Parallel Resistors are different from this. I prefer this method because I can understand it well and used this when I'm in Grade 5. So my question is do we get the same answer if I use this method and my classmates will use the method where they will find its denominator?
kaola
thank you
Mark Donnison
Hi!
Justin chow
hi mark
Mark Donnison
Hi, there is a worked example that shows how to insert your values into the formula and how to take it forwards to an answer. Which bit of the process isn't clear, perhaps we can look at editing the example to highlight this.
no explanation
no explanation on the calculation for the 3 parallel resistor, pointlesss, just hocus pocus and assume everyone gets it
dajake
nice calculations
Sanjay
Really I will your instructions is a very helpful .thanks a lot sir
Tom
Just for fun: task 3 example 1 should be 6 Ohms Also formula for two res in paralel and for more than 2 is exactly the same – if you use the latter for two, but solve it with vulgar fractions without finding smallest denominator, you will get the same formula. So, its also possible to make formulas for each on n numbers of resistors, but its impractical for normal use. P.e. for 3 res Rtot=R1xR2xR3/((R1xR2)(R2xR3)(R1xR3))
Mark Donnison
Hi, thanks for getting in touch. The information that you require is included in the above tutorial. Where it says 'and so on', this indicates that the process is the same for additional resistors. I hope this helps.
sikander lal walia
How to calculate the value of 3 and more resistors in parallel and elaborate the same.
Mark Donnison
Hi Ian, it's difficult to visualise your circuit without seeing it but I will give an answer based on what I think you have. Firstly, you will need to work out the value of the three resistors in parallel (the formula is on the page above). Then, once you have this value you then need to do an in series calculation using the resistor on its own and the result of the first calculation you did to give the total resistance for the circuit. I hope this helps.
Ian De La Cruz
I need your help to find the correct formula . I have 3 parallels and one other on its own. I’m sorry I don’t know the correct terminology but all have a value of 60 ohms . I got an A side and B side : on the A side I have the 60 alone and on the B side I have 3 – 60 ohms. I’m pretty good at math but the formula is missing here. Please help me with a formula to figure out the total resistance
Patrick Lummumba Sunu
This is awesome
danburite
thanks,mark.
Mark Donnison
Hi Yonela, yes you need to use a different formula as is shown in the worked examples.
yonela
for parallel circuit with two resistor we only use that formula in task 2 we do not use it when we have three or more resistors?
Mark Donnison
Hi Bill, you would use the series calculation first to find the combined resistances. So, in this case, R1 becomes R1Total and R2 becomes R2Total and you can then do the parallel calculation as normal. I hope this helps.
Bill
so for parallel circuits with >2 resistors, there is no algebraic equation derived that we can use. We only do the specific calculation to find the specific answer every time?
Mark Donnison
Hi Tom, If your target is 15 the calculation would look like; 1/15 = 1/48 + 1/80 + 1/R. Then rearrange the formula for R, it becomes; 1/15 – 1/48 – 1/80 = 1/R.
Tom
Hi i read this reply to colin and didnt quite understand. What do you do once you have the reciprical values for example my taget is 15 i have 2 resisitors 48 and 80. Recipricals are 1/48=0.208333333 and 1/80=0.0125 what do i do from here?
Manuna Kawkni
very important in my training.
Edwin mothibeli
This is very helpful,thank you for the initiative
Rob Haywood
Hi Colin, Simply work the formula backwards. For series start with the value you want to achieve, subtracting values you have as you go until you reach 0. For parallel what we're dealing with is reciprocal numbers, and they can be reversed. For example 1/33 = 0.30303. 1/0.30303 = 33. So start with the value you want to achieve. Take a resistor value you have and divide 1 by that value to get the reciprocal number. Rob
Colin gilly
What is the formula if I know what resistance I want to achieve but don't have the correct value available. But I do have lots of other value resistors that I might be able to use?
Rob Haywood
HI Elias, It comes down to rounding. We rounded to three significant figures, but if you round shorter than that you will see an answer of around 6, so you have done it right. Given the value of standard resistors anyway in this case you would probably use 6.8 Ohms. Hope that helps.
elias mellber
Hi! I was just wondering about these parallel resistor equations. Isn't the answer to Task 3 question 1 suppose to be 6 instead of 5.95? Or am I just totally lost here? Have a good one!